Praktikum 11 Geostatistika (2)

11.1 Interpoleerimine

Eelmisel korral vaatasime, kuidas kujutada mingi nähtuse intensiivsust eri paikades, kui me kas teame ainult seda, kus nähtuse andmepunktid geograafiliselt paiknevad, või on see ainus, mis meid huvitab. Sel korral vaatame lähemalt, mida teha juhul, kui punktide paiknemise asemel huvitab meid lisaks ka mingi tunnus, mis punkte iseloomustab. Näiteks kui teame mingi hulga vallakohtuprotokollide kohta seda, kui palju sõnu tänapäeva keelel treenitud morfoloogiline analüsaator 19. sajandil kasutatud sõnavormidest ära tundis, saame (küll suhteliselt jämedalt) ennustada, kui tänapäeva eesti keelele sarnast keelt kuskil piirkonnas tollal räägiti, isegi kui meil ei ole konkreetsete geograafiliste punktide kohta andmeid.

Geostatistika abil saame niisiis iseloomustada meid huvitavate atribuutide ruumilist struktuuri ja ennustada nende väärtusi kohtades, kust meil tegelikud vaatlusandmed puuduvad. Selleks, et hinnata mingi nähtuse väärtust kohas, kust meil (valimis) andmeid ei ole, tuleb kasutada interpoleerimist, mis põhinebki ennustamise funktsioonil (prediction).
Sageli kasutatakse interpoleerimist selleks, et luua pidev rastermudel mingist eraldiseisvate punktide hulgast. Interpoleerimiseks on erinevaid meetodeid ning õige valiku tegemine võib olla kohati suhteliselt keeruline. Eelkõige oleneb see andmete iseloomust ja ulatusest ning nähtusest, mida üritame mõista. Tulemus võib samuti meetodist olenevalt suuresti erineda.

Sisuliselt on interpoleerimine ennustav mudeldamine väärtuste hindamiseks mõõtmiskohtade vahel. Teistest meetoditest, nagu näiteks eelmisel korral vaadatud KDE, erinebki see just selle poolest, et interpoleerimine mitte ei iseloomusta mingit andmestikku, vaid pigem ennustab selle põhjal.

11.1.1 Distantsi kaaluv interpoleerimine

Lineaarne distantsipõhine meetod on suhteliselt lihtne, nagu allolevalt jooniselt näha.

Joonis 11.1: Lihtsad interpoleerimise näited. a - kahe punkti ja lineaarse interpoleerimisega D = 15. b - lisades kolmanda punkt ja interpoleerides IDW abil D = 12.5 (Gillings et al. 2020).

Populaarne distantsipõhine meetod on IDW ehk inverse distance weighting (läheduskaalude meetod). Selle puhul kaalutakse punkte vastavalt nendevahelise kauguse ruudule, sest eeldatakse, et punktide väljendatud nähtuse mõju kahaneb, mida kaugemale punktist liikuda. Mida lähemal on punkt, seda suurem on tema kaal. Sellest ka nimi inverse distance weighting. Vaatame korraks ka IDW valemit, et meetodit paremini mõista.

Joonis 11.2: IDW meetodi valem

Valemis tähistab n teadaolevate punktide koguarvu (ülaloleval joonisel b näiteks 3), Z_i iga teadaoleva punkti mingi atribuudi väärtust (näiteks 12, 21 ja 8) ja d_i iga teadaoleva punkti kaugust tundmatust punktist, mille atribuudi väärtust (Z_p) tahame ennustada.

Joonisel oleva punkti D mingi atribuudi väärtuse arvutamiseks seega:

Joonis 11.3: IDW meetodi valemi näide punkti D väärtuse arvutamiseks

Kuna suurima atribuudi väärtusega punkt B asus tundmatust punktist D kaugemal kui lähemad ja madalamate atribuutide väärtustega punktid A ja C, siis B mõju punktile D hinnati väiksemaks ja D väärtus lähemaks seega A ja C väärtustele.

QGISis leiab IDW tööriista, kui valida Processing → Toolbox → Interpolation → IDW interpolation.

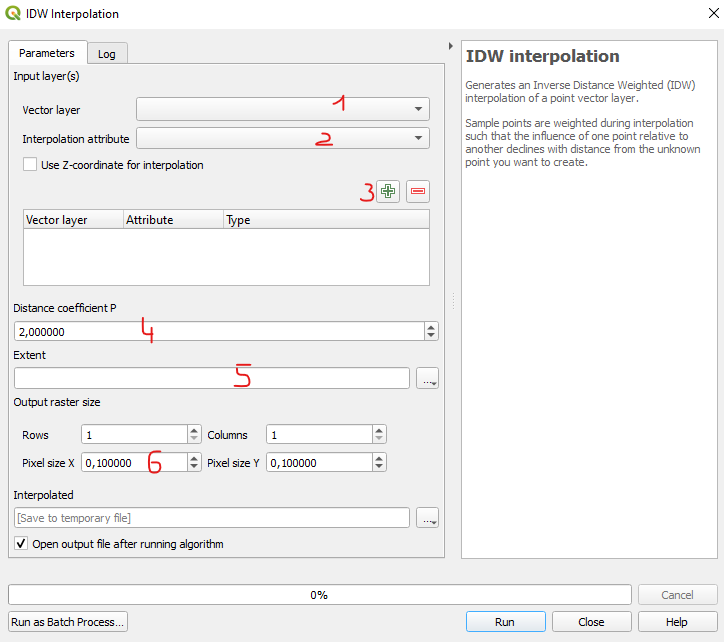
Joonis 11.4: IDW interpoleerimise tööriist QGISis

1 - punktide vektorkiht.
2 - vektorkihi (arvuline!) atribuut, mille väärtusi interpoleerida. Kui tahad interpoleerida kategoorilist tunnust, siis võib mõelda, kas kategooriatel on mingi hierarhia, mispuhul saab kasutada arve 1, 2, 3, 4, 5 jne, või saab teisendada tunnuse binaarseks 1-0 vastanduseks (nt 1 = klass1, 0 = klass2, interpoleeritakse klass1 esinemise tõenäosust).
3 - tuleb vajutada atribuudi lisamiseks.
4 - kauguse koefitsient P ehk power, mis ütleb, millisesse astmesse punktidevaheline kaugus valemis tõsta. Vaikimisi kasutatakse 2. astet ehk ruutuvõtmist (nagu ülal toodud näiteski). Mida suurem on P, seda enam mõju ennustamisel on lähedal asuvatel punktidel ja vähem mõju kaugemale jäävatel ning seda detailsem ja fragmentaarsem on tulemuseks saadav rasterfail. Kui P on 0, siis kauguse põhjal mingit kaalumist ei toimu.
5 - määrab, millises ulatuses rastrit interpoleerida (võib olla nt mingi muu vektorkiht, nagu maakondade vektorkiht).
6 - väljundiks saadava rastri piksli külje suurus (kasutatava CRS-i ühikutes, enamasti meetrites). Mida suurem on mõõtkava (st mida väiksemat ala vaatleme), seda väiksem peaks olema piksli suurus.

GDALi kaudu saab kasutada ka teist IDW-tööriista, mis pakub natuke enam paindlikkust. Näiteks saab seal määrata otsimisraadiuse (kui kaugele jäävaid punkte üldse arvesse võtta) või maksimaalse arvu punkte, mida punkti läheduses arvesse võtta.

11.1.2 Ülesanne 1

Interpoleerime ei ole ja pole varieerumist Andrus Saareste murdeatlase andmete põhjal, kasutades IDW-d. Kuna interpoleerimiseks on vaja arvulist tunnust, peaksime oma binaarse kategoriaalse tunnuse, mis määrab selle, kas kasutati varianti ei ole või pole, teisendama esmalt kujule 0 (ei ole) ja 1 (pole) (vaata avaldiste ja päringute praktikumi materjale, 8.9). Samuti peame kihilt välja jätma punktid, millel keelendi tulbas on väärtus NULL.

Lõika IDW-ga saadud raster kihelkondade piiridesse (Raster → Extraction → Clip Raster by Mask Layer).

11.1.3 Splain (Spline)

Splain (spline) on pidev kõver, mis ühendab punkte. Thin Plate Spline on meetod, kus püütakse splainide abil tekitada minimaalse kumerusega pidevat pinda, mis läbiks kõiki andmestiku punkte, kusjuures punkte kujutatakse ette kolmemõõtmelisena: teame punktide x- ja y- koordinaate ning mingi punktide atribuut, mille väärtusi interpoleerime, annab justkui kõrgusinfo, z-koordinaadi. Pinda üritatakse punktide vahele ja peale sättida niisiis nii, et sel oleks võimalikult vähe kumerust, aga samal ajal oleksid läbitud kõik punktid. Regularized spline lubab kõverale ka väärtuseid, mis on punktide enda väärtustest suuremad või väiksemad (lubame ennustada vaadeldavatest andmetest väljapoole). Tension spline ei lase sellistel kumerustel tekkida.

Joonis 11.5: Splaini meetodi põhimõte. a - regulariseeritud kõrgusväärtusega, mis lubab punkti väärtusest suuremad väärtuseid. b - tension spline, mis hoiab rohkem kinni punktide väärtustest, et luua siledam/ühtlasem pind

QGISis saab splainide abil interpoleerida tööriistaga, mille leiab Processing → Toolbox → SAGA Next Gen → Raster creation tools → Thin Plate Spline. Kui tööriista pole näha, siis installi see pistikprogrammide alt (Plugins → Manage and Install Plugins → Processing Saga NextGen Provider).

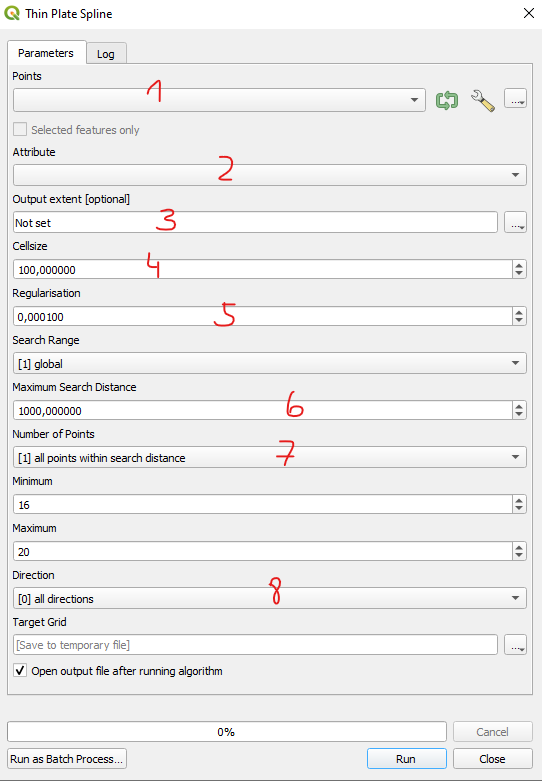
Joonis 11.6: Thin Plate Spline interpoleerimise tööriist QGISis

1 - punktide vektorkiht.
2 - vektorkihi (arvuline) atribuut, mille väärtusi interpoleerida.
3 - määrab, millises ulatuses interpoleerida.
4 - väljundiks saadava rastri piksli lkülje suurus (kasutatava CRS-i ühikutes, enamasti meetrites).
5 - regulariseerimise parameeter. Mida suurem on see parameeter, seda lõdvemalt on splain punktide täpsete asukohtadega seotud (võib olla kasulikum siis, kui olemasolevate punktide koordinaadid ei ole väga täpsed ja kui eeldus on, et vaadeldava nähtuse puhul on üleminekud pigem sujuvad, mitte järsud). Regulariseerimise parameetriga saab kontrollida rasterkihi ennustuste ülesobitamist.
6 - otsimisraadius CRSi originaalühikutes (nt meetrites).
7 - mitut punkti iga piksli väärtuse arvutamisel arvestada. Mida rohkem punkte arvesse võtta, seda kaugemaid punkte saab rastri arvutamisel arvestada ja seda sujuvamad on rastri üleminekud.
8 - mis suunas punkte arvestada.

11.1.4 Ülesanne 2

Interpoleerime samu atlase andmeid nüüd Thin Plate Spline meetodiga. Katsetame eri parameetrite väärtustega (eeskätt eri regulariseerimise parameetriga).

11.1.5 Ülesanne 3

Interpoleerime nüüd nii IDW-ga kui ka TPS-iga ei ole ja pole eituskonstruktsioonide varieerumist Eesti murretes, kasutades atlase levikuandmete asemel murdekorpuse sagedusandmeid. Sagedusandmed võimaldavad interpoleerimisel kasutada 0 ja 1 asemel ka vahepealseid väärtusi (ei ole või pole osakaalusid), seega võiks raster tulla sujuvam ja nüansseeritum. Teisalt on meil korpusandmete puhul kasutada iga kihelkonna kohta sisuliselt ainult ühe punkti andmed.

• Esmalt tuleb kasutuse osakaalude CSV-tabel liita kihelkondade ruumiandmetega (NB! Kontrolli kihelkondade nimesid, vt 8.6.1).
  
• Kuna interpoleerimiseks vajame punkte, mitte polügoone, siis tuleb need seejärel leida osakaaludega kihelkondade kihi põhjal. Selleks leiame kihelkondade keskpunktid ehk tsentroidid (Vector → Geometry Tools → Centroids).
  
• Lõpetuseks tuleks välja jätta punktid (kihelkonnad), kust osakaalude andmed puuduvad.

Nüüd interpoleerime punktandmeid erinevate meetoditega, lõikame saadud rastrid kihelkondade piiridesse ja värvime sama värvipaletiga. Võrdleme erinevusi.

11.2 Voronoi polügoonid

Kui meil on tegemist kategoriaalse (st mittearvulise) atribuudiga (nt Keelend võib olla ei ole või pole) ja me ei taha neid kunstlikult arvulisteks vastandusteks muuta, siis saame kategooriate levikut kujutada ka nn Voronoi polügoonide abil (tuntud ka kui Thiesseni polügoonid). Sel puhul jagatakse punktandmete ümber asuv pind väikesteks “keskusteks” nii, et igas keskuses asuv suvaline punkt (mille väärtust me ei tea) kuuluks just selle keskuse juurde. Iga tegeliku andmepunkti ümber jääv ala kannab niisiis andmepunktiga samu atribuute ja atribuudi väärtus võiks esineda seega tervesse alasse jäävatel suvalistel punktidel. Alad saab värvida vastavalt sellele atribuudile.

• Valime Processing → Toolbox → Vector geometry → Voronoi polygons.
  
• Input layer olgu ei ole ja pole levikut kujutava murdeatlase punktikiht. Vajutame Run.
  
• Saadud kihi lõikame kihelkondade kihi piiridesse: Vector → Geoprocessing Tools → Clip, Input layer olgu Voronoi polygons ja Overlay layer kihelkondade vektorkiht. Vajutame Run.
  
• Saadud kihil Clipped värvime polügoonid vastavalt atribuudile, mis ütleb, kas polügooni alla jääval alal võidaks kasutada pigem varianti ei ole või pole: Symbology → Categorized.

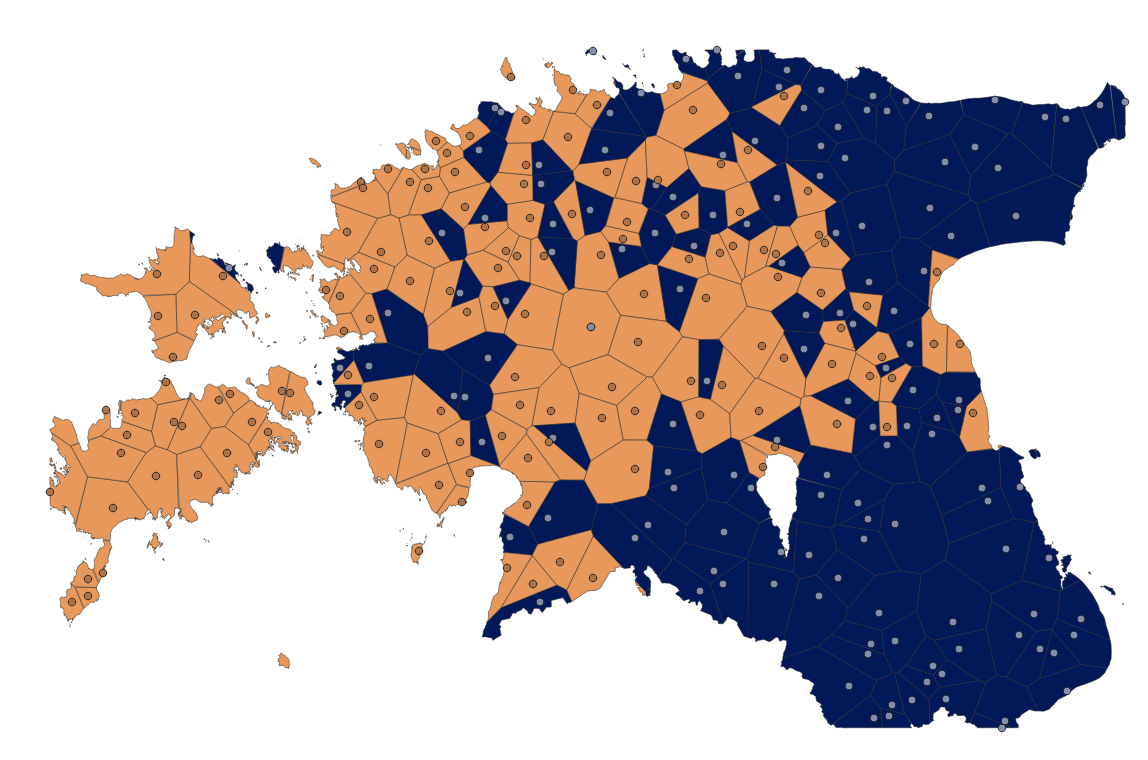
Joonis 11.7: Voronoi polügoonide klassifitseerimine ei ole ja pole kasutuse põhjal

11.3 Muud meetodid

Ehkki siin jõudsime käsitleda vaid kolme levinumat interpoleerimise meetodit, võimaldab QGIS (täpsemalt SAGA GIS) kasutada veel palju muidki algoritme, nt kriging, B-spline approximation jpt. Tasub proovida erinevaid meetodeid ja erinevaid sätteid, selleks et saada interpoleeritud raster, mis konkreetsetele andmetele kõige paremini sobiks.

SAGA GISi abil on võimalik kasutada ka muid statistilisi meetodeid, näiteks regressiooni.